Симулятор квадрокоптера: симуляция щёточных DC моторов
Не думал о подобном ранее, но чуток покопавшись понял, что всё достаточно просто )
(Я далеко не физик/электронщик и могу что-то сам не так понимать или описывать, но тем не менее)
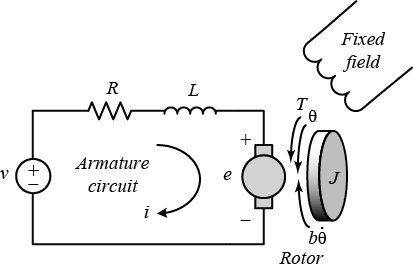
Щёточный DC схематически можно представить так:
R – сопротивление обмотки ротора.
L – индуктивность обмотки ротора
e – обратная ЭДС обмоток ротора.
J – момент инерции ротора
Из за вращения ротора в статичном магнитном поле в его обмотках появляется обратная ЭДС, создающая обратное напряжение в обмотках, которое ограничивает максимальные обороты движка (но не только оно ограничивает). Зависит линейно от угловой скорости ротора.
Так же есть ЭДС самоиндукции, появляющаяся при изменении тока, проходящего по обмоткам.
E = – L* (dI/dt)
– как видно тут участвует производная тока и самоиндукция будет влиять на работу мотора только когда ток меняется, КЭП.
e – величина линейная, зависит от угловой скорости ротора, равна k_e * w. k_e – константа обратной ЭДС.
Пользуясь вторым правилом Кирхгофа можно записать уравнение напряжения в моторе:
Vs = R*I + L*(dI/dt) + e;
тут Vs – напряжение питания мотора.
Не сложно переписать уравнение так, что бы выразить производную тока:
dI/dt = (Vs – (R*I) – e) / L;
Уже хорошо, но кроме тока нам интересны ещё и обороты движка, и крутящий момент же.
Для начала можно описать, так сказать, уравнение равновесия крутящих моментов:
Me = Mm + Mf + Ml
Me = электрический крутящий момент, т.е. момент, сгенеренный обмотками ротора.
Mf – момент трения ротора, линейно зависит от угловой скорости, k_f * w,
Ml – момент внешней нагрузки на ротор.
w – угловая скорость ротора [рад/с]
т.е. Me = J*(dw/dt) + k_f*w + Ml;
Тут есть важная штука: “электрический” момент линейно зависит от тока на обмотках якоря и его коэффициент является одной из важнейших характеристик моторов. То есть “электрический” момент (Me) = k_t * I;
k_t * I = J*(dw/dt) + k_f*w + Ml;
Выразим производную угловой скорости ротора:
dw/dt = (k_t*I – k_f*w – Ml) / J
Теперь у нас есть 2 дифференциальных уравнения, которые можно проинтегрировать и получить графики работы движка.
Для проверки себя я заскринил реальный график реального движка, подложил в юнити в виде плоскости с текстурой под свой рисуемый график.
Изначально ничего не сошлось, т.к. я не корректно вбил коэффициенты. Плюс к тому не ясно для какого точно напряжения построен график и какое точно сопротивление было у движка, для которого он строился. Коэффициенты то есть в даташите, но они немного отличаются от того, что на графике!
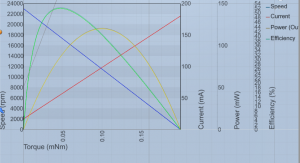
Что бы график сошёлся идеально, необходимо было крутить несколько коэффициентов. Это достаточно геморно и потому я использовал алгоритм оптимизации Левенберга-Марквардта для автоматической подстройки параметров ))) Критериями ошибок стали максимумы и производные графиков тока и оборотов мотора, а так же разница между идеальными и реальными экстремумами графиков мощности и эффективности, вот что получилось:
Тут gizmo используется для отрисовки графиков, под ними подложка с текстурой реальных графиков. Всё вполне совпадает )
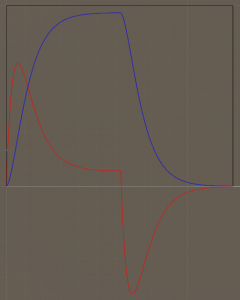
А вот график по времени. Сначала включается питание мотора и потом по достижению максимальных оборотов питание отключается. Видны 2 всплеска на графиках – большой пусковой ток и выброс в отрицательную сторону при выключении. Синий график – обороты, красный – ток.